Maths questions or calculations that are incorrect or confusing
|
Some maths questions published in books or on the internet are confusing, written incorrectly, or easily misunderstood. Here are some of them. Can you spot the mistakes or say how they can be corrected or improved? Have you come across other examples? Let Dr Singh know. |
Image credit:
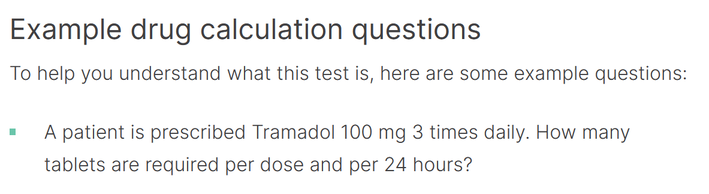
Q1 What is wrong with the question below? (Ref)
Answer: It does not state the weight of a tablet. If each is 25mg, then each dose requires 4 tablets. If each is 50mg, then each dose requires 2 tablets. If each is 100mg, then each dose requires 1 tablet.
Answer: It does not state the weight of a tablet. If each is 25mg, then each dose requires 4 tablets. If each is 50mg, then each dose requires 2 tablets. If each is 100mg, then each dose requires 1 tablet.
Q 2 What is wrong with the question below? (Ref).
Answer: It says "probability" but then says "1 in 4". "1 in 4" is an expression of proportion not probability, so the writer is confusing proportion with probability. The writer should have written "1:3" instead of "1 in 4".
Answer: It says "probability" but then says "1 in 4". "1 in 4" is an expression of proportion not probability, so the writer is confusing proportion with probability. The writer should have written "1:3" instead of "1 in 4".
Q 3 What is wrong with the question below? (Ref: "Test your numerical aptitude" p72 Q19; ISBN9780749450649; 2007; Kogan Page; Barrett).
Answer: None of the choices is correct. d) is partly correct because it has the right figures, but they are written back-to-front. It would be correct if it said "6:14", because that matches the order of numbers in the question.
Answer: None of the choices is correct. d) is partly correct because it has the right figures, but they are written back-to-front. It would be correct if it said "6:14", because that matches the order of numbers in the question.
"A ratio of 1 1/2 to 3 1/2 is the same as...?" a) 2:3 b) 5:12 c) 8:15 d) 14:6
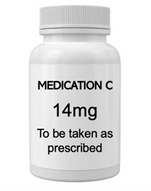
Q 4 What is wrong with the question below? (Ref: NHS Numeracy and Literacy Test Questions & Answers!)
Answer: This is how the question actually appeared, but it is confusing because it fails to say whether the 42mg is for 1 day or for 7 days. If read as stated, then it means just 3 tablets to last 7 days, which is nonsense, so the alternative is 42mg PER DAY. The question should say "42mg per day of medication C" The question could also be improived by saying EACH tablet is 14mg, because otherwise this must be assumed.
Answer: This is how the question actually appeared, but it is confusing because it fails to say whether the 42mg is for 1 day or for 7 days. If read as stated, then it means just 3 tablets to last 7 days, which is nonsense, so the alternative is 42mg PER DAY. The question should say "42mg per day of medication C" The question could also be improived by saying EACH tablet is 14mg, because otherwise this must be assumed.
Referring to the image above, "A patient has been prescribed 42mg of medication C over a 7 day period. How many tablets should they be administered in total?"
Q 5 What is wrong with the statement below? (Ref: "Test your numerical aptitude" p15 Q 5; ISBN9780749450649; 2007; Kogan Page; Barrett).
Answer: It would be less confusing if the writer had said "proportion is a special type of ratio" to distinguish it from ratios. That distinction is necessary because proportion considers a part in relation to the whole, whereas the common use of the word "ratio" is the relationship of a part to another part and NOT its relation to the whole. The second confusion is in the expression "1:2" A colon is the usual way to express RATIOS and so to avoid mistaking proportions for ratios, I think it is far better to express proportions as fractions, such as 1/2 in this question, and NOT to use a colon. A second reason to avoid using a colon is because converting a ratio to a proportion requires the denominator to be the sum of the figures separated by a colon. In the answer, the proportion is written as 1:2, and so the proportion of articles that are newspapers would be calculated as 1/(1+2) or 1/3. 1/3 is not the correct answer because the answer is 1/2 One might argue that the expression 1:2 is a proportion though it appears to be a common ratio and so to convert that expression to a fraction, one must NOT add the two figures on either side of the colon but simply place the right-hand figure as the denominator and the left as the numerator. To illustrate converting from ratios to proportions and how to express them, see this video clip at 1min 38 sec (Converting Ratios into Proportions KS2) and see this clip (The difference between ratio and proportion. Don’t get confused!) to understand the distinction between (and so avoid the confusion) ratios and proportions.
"Proportion is another word for ratio. It is a part of the whole or total number." Books, newspapers, and magazines are in the ratio 15:25:10 "What proportion of the number of articles are newspapers?" "Answer: 1:2 (or 1/2)"
Answer: It would be less confusing if the writer had said "proportion is a special type of ratio" to distinguish it from ratios. That distinction is necessary because proportion considers a part in relation to the whole, whereas the common use of the word "ratio" is the relationship of a part to another part and NOT its relation to the whole. The second confusion is in the expression "1:2" A colon is the usual way to express RATIOS and so to avoid mistaking proportions for ratios, I think it is far better to express proportions as fractions, such as 1/2 in this question, and NOT to use a colon. A second reason to avoid using a colon is because converting a ratio to a proportion requires the denominator to be the sum of the figures separated by a colon. In the answer, the proportion is written as 1:2, and so the proportion of articles that are newspapers would be calculated as 1/(1+2) or 1/3. 1/3 is not the correct answer because the answer is 1/2 One might argue that the expression 1:2 is a proportion though it appears to be a common ratio and so to convert that expression to a fraction, one must NOT add the two figures on either side of the colon but simply place the right-hand figure as the denominator and the left as the numerator. To illustrate converting from ratios to proportions and how to express them, see this video clip at 1min 38 sec (Converting Ratios into Proportions KS2) and see this clip (The difference between ratio and proportion. Don’t get confused!) to understand the distinction between (and so avoid the confusion) ratios and proportions.
"Proportion is another word for ratio. It is a part of the whole or total number." Books, newspapers, and magazines are in the ratio 15:25:10 "What proportion of the number of articles are newspapers?" "Answer: 1:2 (or 1/2)"
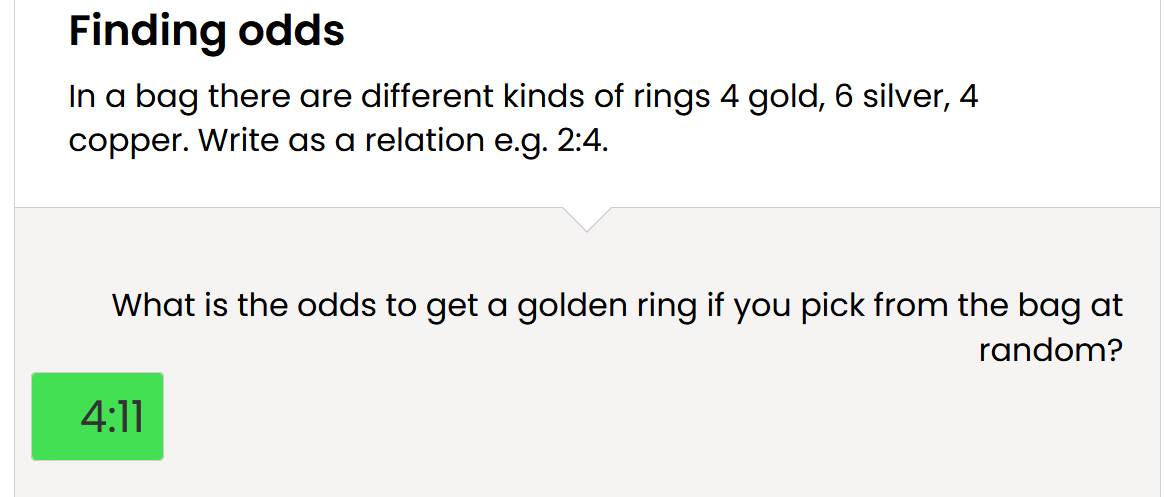
Q 6 What is wrong with the answer below of 4:11 provided by the website manager? (Ref: mathplanet.com )
Answer: Stating "odds" means showing as the numerator of a fraction, the number of events that meet the criteria and showing as the denominator, the number of events that do not meet the criteria. Looking at the Q, there are 4 chances of picking gold and 10 chances of picking some other colour, so the odds are stated as 4:10, yet the website says that is incorrect (see right-hand image below) and says the correct odds are 4:11
Answer: Stating "odds" means showing as the numerator of a fraction, the number of events that meet the criteria and showing as the denominator, the number of events that do not meet the criteria. Looking at the Q, there are 4 chances of picking gold and 10 chances of picking some other colour, so the odds are stated as 4:10, yet the website says that is incorrect (see right-hand image below) and says the correct odds are 4:11
|
|
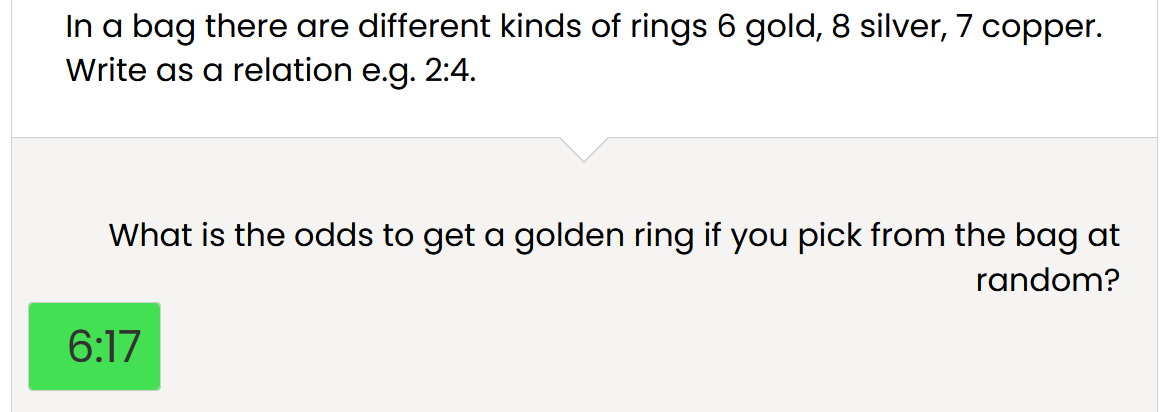
Q 7 What is wrong with the answer below of 6:17 provided by the website manager? (Ref: mathplanet.com )
Answer: Stating "odds" means showing as the numerator of a fraction, the number of events that meet the criteria and showing as the denominator, the number of events that do not meet the criteria. Looking at the Q, there are 6 chances of picking gold and 15 chances of picking some other colour, so the odds are stated as 6:15, yet the website says that is incorrect and says the correct odds are 6:17
Answer: Stating "odds" means showing as the numerator of a fraction, the number of events that meet the criteria and showing as the denominator, the number of events that do not meet the criteria. Looking at the Q, there are 6 chances of picking gold and 15 chances of picking some other colour, so the odds are stated as 6:15, yet the website says that is incorrect and says the correct odds are 6:17
|
|
Q 8 What is wrong with the answer of £400 to the question below? (Ref Highfield, functional skills maths Level 2 mock paper, calculator, Q9, Jan 2023)
A laptop costs £320 in a sale. The laptop was 20% more expensive before the sale. How much was the laptop before the sale?
Answer: The marking scheme says the answer is £400 and the publisher insists the answer is £400 because 20% off £400 is £320. I argued that the 20% refers to the reduced price (not to the original price) so that should be increased - to give a pre-sale price of £384. The difference of opinion on what is correct therefore rests on what the "20%" refers to? In other words, a badly-worded question.
A laptop costs £320 in a sale. The laptop was 20% more expensive before the sale. How much was the laptop before the sale?
Answer: The marking scheme says the answer is £400 and the publisher insists the answer is £400 because 20% off £400 is £320. I argued that the 20% refers to the reduced price (not to the original price) so that should be increased - to give a pre-sale price of £384. The difference of opinion on what is correct therefore rests on what the "20%" refers to? In other words, a badly-worded question.
Q 9 The question below wants to know which of the tickets is the cheapest option for a commuter? The answer says the monthly ticket is the cheapest option. Do you agree or disagree? (Ref Highfield, functional skills maths Level 2 mock paper, calculator, Q13, Jan 2023)
Answer: The monthly option is correct, because the question says 3 months is 13 weeks. Recognising and accepting that the 3 months is made of 13 NOT 12 weeks, is a crucial point, and easily overlooked. The question is not badly written but it needs to be carefully read because otherwise one could add an extra week to the 3 months (assuming it is made of 12 weeks) to make 13 weeks, so buy one weekly ticket in addition to 3 monthly tickets. That is what I did and why I was wrong.
Answer: The monthly option is correct, because the question says 3 months is 13 weeks. Recognising and accepting that the 3 months is made of 13 NOT 12 weeks, is a crucial point, and easily overlooked. The question is not badly written but it needs to be carefully read because otherwise one could add an extra week to the 3 months (assuming it is made of 12 weeks) to make 13 weeks, so buy one weekly ticket in addition to 3 monthly tickets. That is what I did and why I was wrong.
Q 10 The question below wants to know what the employee's total pay for working was? Is it written clearly, or is it ambiguous, i.e., did the employee work on Saturday? (Ref Highfield, functional skills maths Level 2 mock paper, calculator, Q14, Jan 2023)
Answer: It is badly written because it is not clear whether Saturday was worked or not. The question should have said “inclusive” after “Saturday” or said “worked six days and 7.5…” to avoid ambiguity
Answer: It is badly written because it is not clear whether Saturday was worked or not. The question should have said “inclusive” after “Saturday” or said “worked six days and 7.5…” to avoid ambiguity
Something is not right with Poundland's figures in the product for sale below. Can you spot the mistake? Send your Comments using the box below.
Something is not right with the land area figures in the right-hand column below. Can you spot the mistake? Send your Comments using the box below. Ref: https://www.nobroker.in/blog/land-measurement-units/
Something is not right with the land area figures below. Can you spot the mistake? Send your Comments using the box below. Ref: https://www.nobroker.in/blog/land-measurement-units/
The book "The primary teacher's guide to financial education" (ISBN 9781407127996). says (on page 27):
"The note with the most zeros on it is the Zimbabwean 100 trillion (100, 000, 000, 000, 000) dollar note (issued in 2009)."
In the UK, until Dec 1974, a trillion was not written with this number of zeros. Can you say how many were used?
Answer: In the UK a trillion was 1 billion x billion, i.e., 1 followed by 24 zeros, because 1 billion was 1 million x 1 million, i.e., 1 followed by 12 zeros. Sadly, in 1974, the UK adopted the international convention of writing large numbers (according to this post: https://www.quora.com/How-many-zeros-does-a-trillion-have-the-UK ).
"The note with the most zeros on it is the Zimbabwean 100 trillion (100, 000, 000, 000, 000) dollar note (issued in 2009)."
In the UK, until Dec 1974, a trillion was not written with this number of zeros. Can you say how many were used?
Answer: In the UK a trillion was 1 billion x billion, i.e., 1 followed by 24 zeros, because 1 billion was 1 million x 1 million, i.e., 1 followed by 12 zeros. Sadly, in 1974, the UK adopted the international convention of writing large numbers (according to this post: https://www.quora.com/How-many-zeros-does-a-trillion-have-the-UK ).
|
|
Enter your name and email address, then press the Submit button to send your comments.
|